When Is Correlation Transitive?

Given two unit vectors {v,w}

in a real inner product space, one can define the correlation between these vectors to be their inner product ${\langle v, w \rangle}$ , or in more geometric terms, the cosine of the angle ${\angle(v,w)}$ subtended by {v}

and

. By the Cauchy-Schwarz inequality, this is a quantity between {-1}

and

, with the extreme positive correlation {+1}

occurring when {v,w}

are identical, the extreme negative correlation {-1}

occurring when {v,w}

are diametrically opposite, and the zero correlation {0}

occurring when {v,w}

are orthogonal. This notion is closely related to the notion of correlation between two non-constant square-integrable real-valued random variables {X,Y}

, which is the same as the correlation between two unit vectors {v,w}

lying in the Hilbert space ${L^2(\Omega)}$ of square-integrable random variables, with {v}

being the normalisation of {X}

defined by subtracting off the mean ${\mathbf{E} X}$ and then dividing by the standard deviation of {X}

, and similarly for {w}

and

One can also define correlation for complex (Hermitian) inner product spaces by taking the real part ${\hbox{Re} \langle , \rangle}$ of the complex inner product to recover a real inner product.

While reading the (highly recommended) recent popular maths book "How not to be wrong", by my friend and co-author Jordan Ellenberg, I came across the (important) point that correlation is not necessarily transitive: if {X}

correlates with {Y}

, and

correlates with {Z}

, then this does not imply that {X}

correlates with {Z}

. A simple geometric example is provided by the three unit vectors

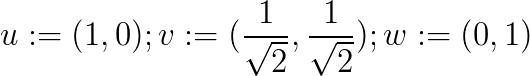
$\displaystyle u := (1,0); v := (\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}); w := (0,1)$

in the Euclidean plane ${{\bf R}^2}$ : {u}

and

have a positive correlation of ${\frac{1}{\sqrt{2}}}$ , as does {v}

and

, but

and

are not correlated with each other. Or: for a typical undergraduate course, it is generally true that good exam scores are correlated with a deep understanding of the course material, and memorising from flash cards are correlated with good exam scores, but this does not imply that memorising flash cards is correlated with deep understanding of the course material.

However, there are at least two situations in which some partial version of transitivity of correlation can be recovered. The first is in the "99%" regime in which the correlations are very close to {1}

: if

are unit vectors such that {u}

is very highly correlated with {v}

, and

is very highly correlated with {w}

, then this does imply that {u}

is very highly correlated with {w}

. Indeed, from the identity

$\displaystyle \| u-v \| = 2^{1/2} (1 - \langle u,v\rangle)^{1/2}$

(and similarly for {v-w}

and

) and the triangle inequality

$\displaystyle \|u-w\| \leq \|u-v\| + \|v-w\|,$

we see that

Thus, for instance, if ${\langle u, v \rangle \geq 1-\varepsilon}$ and ${\langle v,w \rangle \geq 1-\varepsilon}$ , then ${\langle u,w \rangle \geq 1-4\varepsilon}$ . This is of course closely related to (though slightly weaker than) the triangle inequality for angles:

$\displaystyle \angle(u,w) \leq \angle(u,v) + \angle(v,w).$

Remark 1 (Thanks to Andrew Granville for conversations leading to this observation.) The inequality (1) also holds for sub-unit vectors, i.e. vectors with ${\|u\|, \|v\|, \|w\| \leq 1}$ . This comes by extending in directions orthogonal to all three original vectors and to each other in order to make them unit vectors, enlarging the ambient Hilbert space if necessary. More concretely, one can apply (1) to the unit vectors

$\displaystyle (u, \sqrt{1-\|u\|^2}, 0, 0), (v, 0, \sqrt{1-\|v\|^2}, 0), (w, 0, 0, \sqrt{1-\|w\|^2})$

in ${H \times {\bf R}^3}$ .

But even in the " ${1\%}$ " regime in which correlations are very weak, there is still a version of transitivity of correlation, known as the van der Corput lemma, which basically asserts that if a unit vector {v}

is correlated with many unit vectors ${u_1,\dots,u_n}$ , then many of the pairs ${u_i,u_j}$ will then be correlated with each other. Indeed, from the Cauchy-Schwarz inequality

$\displaystyle |\langle v, \sum_{i=1}^n u_i \rangle|^2 \leq \|v\|^2 \| \sum_{i=1}^n u_i \|^2$

we see that

Thus, for instance, if ${\langle v, u_i \rangle \geq \varepsilon}$ for at least ${\varepsilon n}$ values of ${i=1,\dots,n}$ , then (after removing those indices {i}

for which ${\langle v, u_i \rangle < \varepsilon}$ ) ${\sum_{i,j} \langle u_i, u_j \rangle}$ must be at least ${\varepsilon^4 n^2}$ , which implies that ${\langle u_i, u_j \rangle \geq \varepsilon^4/2}$ for at least ${\varepsilon^4 n^2/2}$ pairs {(i,j)}

. Or as another example: if a random variable {X}

exhibits at least ${1\%}$ positive correlation with {n}

other random variables ${Y_1,\dots,Y_n}$ , then if

10,000}" />, at least two distinct ${Y_i,Y_j}$ must have positive correlation with each other (although this argument does not tell you which pair ${Y_i,Y_j}$ are so correlated). Thus one can view this inequality as a sort of `pigeonhole principle" for correlation.

A similar argument (multiplying each ${u_i}$ by an appropriate sign ${\pm 1}$ ) shows the related van der Corput inequality

and this inequality is also true for complex inner product spaces. (Also, the ${u_i}$ do not need to be unit vectors for this inequality to hold.)

Geometrically, the picture is this: if {v}

positively correlates with all of the ${u_1,\dots,u_n}$ , then the ${u_1,\dots,u_n}$ are all squashed into a somewhat narrow cone centred at {v}

. The cone is still wide enough to allow a few pairs ${u_i, u_j}$ to be orthogonal (or even negatively correlated) with each other, but (when {n}

is large enough) it is not wide enough to allow all of the ${u_i,u_j}$ to be so widely separated. Remarkably, the bound here does not depend on the dimension of the ambient inner product space; while increasing the number of dimensions should in principle add more "room" to the cone, this effect is counteracted by the fact that in high dimensions, almost all pairs of vectors are close to orthogonal, and the exceptional pairs that are even weakly correlated to each other become exponentially rare. (See this previous blog post for some related discussion; in particular, Lemma 2 from that post is closely related to the van der Corput inequality presented here.)

A particularly common special case of the van der Corput inequality arises when {v}

is a unit vector fixed by some unitary operator {T}

, and the ${u_i}$ are shifts ${u_i = T^i u}$ of a single unit vector {u}

. In this case, the inner products ${\langle v, u_i \rangle}$ are all equal, and we arrive at the useful van der Corput inequality

(In fact, one can even remove the absolute values from the right-hand side, by using (2) instead of (4).) Thus, to show that {v}

has negligible correlation with {u}

, it suffices to show that the shifts of {u}

have negligible correlation with each other.

Here is a basic application of the van der Corput inequality:

Proposition 2 (Weyl equidistribution estimate) Let ${P: {\bf Z} \rightarrow {\bf R}/{\bf Z}}$ be a polynomial with at least one non-constant coefficient irrational. Then one has

$\displaystyle \lim_{N \rightarrow \infty} \frac{1}{N} \sum_{n=1}^N e( P(n) ) = 0,$

where ${e(x) := e^{2\pi i x}}$ .

Note that this assertion implies the more general assertion

$\displaystyle \lim_{N \rightarrow \infty} \frac{1}{N} \sum_{n=1}^N e( kP(n) ) = 0$

for any non-zero integer {k}

(simply by replacing {P}

), which by the Weyl equidistribution criterion is equivalent to the sequence ${P(1), P(2),\dots}$ being asymptotically equidistributed in ${{\bf R}/{\bf Z}}$ .

Proof: We induct on the degree {d}

of the polynomial {P}

, which must be at least one. If {d}

is equal to one, the claim is easily established from the geometric series formula, so suppose that

1}" /> and that the claim has already been proven for {d-1}

. If the top coefficient ${a_d}$ of ${P(n) = a_d n^d + \dots + a_0}$ is rational, say ${a_d = \frac{p}{q}}$ , then by partitioning the natural numbers into residue classes modulo {q}

, we see that the claim follows from the induction hypothesis; so we may assume that the top coefficient ${a_d}$ is irrational.

In order to use the van der Corput inequality as stated above (i.e. in the formalism of inner product spaces) we will need a non-principal ultrafilter {p}

(see e.g this previous blog post for basic theory of ultrafilters); we leave it as an exercise to the reader to figure out how to present the argument below without the use of ultrafilters (or similar devices, such as Banach limits). The ultrafilter {p}

defines an inner product ${\langle, \rangle_p}$ on bounded complex sequences ${z = (z_1,z_2,z_3,\dots)}$ by setting

$\displaystyle \langle z, w \rangle_p := \hbox{st} \lim_{N \rightarrow p} \frac{1}{N} \sum_{n=1}^N z_n \overline{w_n}.$

Strictly speaking, this inner product is only positive semi-definite rather than positive definite, but one can quotient out by the null vectors to obtain a positive-definite inner product. To establish the claim, it will suffice to show that

$\displaystyle \langle 1, e(P) \rangle_p = 0$

for every non-principal ultrafilter {p}

Note that the space of bounded sequences (modulo null vectors) admits a shift {T}

, defined by

$\displaystyle T (z_1,z_2,\dots) := (z_2,z_3,\dots).$

This shift becomes unitary once we quotient out by null vectors, and the constant sequence {1}

is clearly a unit vector that is invariant with respect to the shift. So by the van der Corput inequality, we have

$\displaystyle |\langle 1, e(P) \rangle_p| \leq \frac{1}{n^2} \sum_{1 \leq i,j \leq n} |\langle T^i e(P), T^j e(P) \rangle_p|$

for any ${n \geq 1}$ . But we may rewrite ${\langle T^i e(P), T^j e(P) \rangle = \langle 1, e(T^j P - T^i P) \rangle_p}$ . Then observe that if ${i \neq j}$ , ${T^j P - T^i P}$ is a polynomial of degree {d-1}